面试基础总结
一. 操作系统
1.1 并行和并发
并发:在操作系统中,某一时间段,几个程序在同一个CPU上运行,但在任意一个时间点上,只有一个程序在CPU上运行。
并行:当操作系统有多个CPU时,一个CPU处理A线程,另一个CPU处理B线程,两个线程互相不抢占CPU资源,可以同时进行,这种方式成为并行。
知乎的例子:
- 你吃饭吃到一半,电话来了,你一直到吃完了以后才去接,这就说明你不支持并发也不支持并行。
- 你吃饭吃到一半,电话来了,你停了下来接了电话,接完后继续吃饭,这说明你支持并发。
- 你吃饭吃到一半,电话来了,你一边打电话一边吃饭,这说明你支持并行。
1.2 进程和线程
1.2.1 进程
进程是资源分配的基本单位,理解为一个程序。所以我们一般都要求进程池的进程数小于等于CPU的核心数。
如果问单核CPU能否运行多进程?答案又是肯定的。单核CPU也可以运行多进程,只不过不是同时的,而是极快地在进程间来回切换实现的多进程。进程拥有自己的地址空间,全局变量,文件描述符,各种硬件等等资源。
1.2.2 线程
线程:线程是依赖于进程的。如果说进程和进程之间相当于程序与程序之间的关系,那么线程与线程之间就相当于程序内的任务和任务之间的关系。
一个程序内包含了多种任务。加上了线程之后,线程能够共享进程的大部分资源,并参与CPU的调度。意味着它能够在进程间进行切换,实现并发。
1.2.3 为什么要用多进程,适用条件
总是在运行一个进程上的任务,就会出现一个现象。就是任务不一定总是在执行 ”计算型“ 的任务,会有很大可能是在执行网络调用,阻塞了,CPU 岂不就浪费了?
因此,多进程适用于CPU密集型任务(各种循环处理、计算等等)。多线程适用于IO密集型任务(文件处理、网络爬虫等)。
1.2.4 多进程通信
管道pipe:管道是一种半双工的通信方式,数据只能单向流动,而且只能在具有亲缘关系的进程间使用。进程的亲缘关系通常是指父子进程关系。类似于python的multiprocessing.Pipe()
消息队列MessageQueue:消息队列是由消息的链表,存放在内核中并由消息队列标识符标识。消息队列克服了信号传递信息少、管道只能承载无格式字节流以及缓冲区大小受限等缺点。类似于python的multiprocessing.Queue()
共享存储SharedMemory:共享内存就是映射一段能被其他进程所访问的内存,这段共享内存由一个进程创建,但多个进程都可以访问。共享内存是最快的 IPC 方式,它是针对其他进程间通信方式运行效率低而专门设计的。它往往与其他通信机制,如信号两,配合使用,来实现进程间的同步和通信。
1.2.5 python的多线程是真的多线程么
Python在设计之初就考虑要在主循环中,同时只有一个线程在执行,就像单CPU的系统中运行多个进程那样,内存中可以存放多个程序,但任意时刻,只有一个程序在CPU中运行。同样地,虽然Python解释器可以运行多个线程,只有一个线程在解释器中运行。
Python虚拟机的访问由全局解释器锁(GIL)来控制,正是这个锁能保证同时只有一个线程在运行。
Python的多进程多线程测试:
-
在一个4核CPU上开4线程,发现电脑的CPU利用率没有占满,大致相当于单核水平。
-
在一个4核CPU上开4进程,发现CPU直接飙到了100%,说明进程是可以利用多核的!
Python多线程相当于单核多线程,多线程有两个好处:CPU并行,IO并行,单核多线程相当于自断一臂。所以,在Python中,可以使用多线程,但不要指望能有效利用多核。
1.2.6 多线程如何保证线程安全
当多个线程同时操作同一个共享全局变量的时候,就容易出现线程安全问题,线程安全问题只会影响到线程对同一个共享的全局变量的写操作。
利用线程锁来保证同一个时刻,有且仅有一个线程对共享的全局变量进行写操作。且开始写操作前,需要加锁,完成后,需要解锁,让其他线程再对其进行写操作。
1.2.7 死锁问题
死锁是指两个或两个以上的进程(线程)在执行过程中,由于竞争资源或者由于彼此通信而造成的一种阻塞的现象,若无外力作用,它们都将无法推进下去。此时称系统处于死锁状态或系统产生了死锁,这些永远在互相等待的进程(线程)称为死锁进程(线程)。
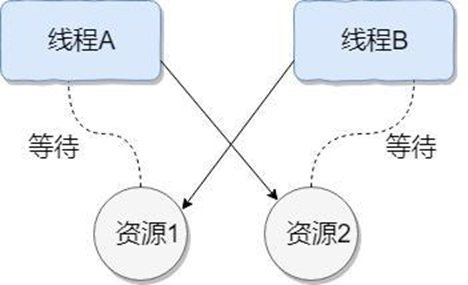
死锁的4个必要条件:
- 互斥条件:线程(进程)对于所分配到的资源具有排它性,即一个资源只能被一个线程(进程)占用,直到被该线程(进程)释放。
- 请求与保持条件:一个线程(进程)因请求被占用资源而发生阻塞时,对已获得的资源保持不放。
- 不剥夺条件:线程(进程)已获得的资源在末使用完之前不能被其他线程强行剥夺,只有自己使用完毕后才释放资源。
- 循环等待条件:当发生死锁时,所等待的线程(进程)必定会形成一个环路(类似于死循环),造成永久阻塞
如何避免死锁?
只要破坏产生死锁的四个条件中的其中一个就可以了。
- 破坏互斥条件:这个条件我们没有办法破坏,因为我们用锁本来就是想让他们互斥的(临界资源需要互斥访问)。
- 破坏请求与保持条件:一次性申请所有的资源。
- 破坏不剥夺条件:占用部分资源的线程进一步申请其他资源时,如果申请不到,可以主动释放它占有的资源。
- 破坏循环等待条件:靠按序申请资源来预防。按某一顺序申请资源,释放资源则反序释放。破坏循环等待条件。
1.3 同步和异步
1.3.1 阻塞和非阻塞
-
阻塞:指调用线程或者进程被操作系统挂起。
-
非阻塞:指调用线程或者进程不会被操作系统挂起。
1.3.2 同步和异步
同步是阻塞模式,异步是非阻塞模式。
- 同步:指一个进程在执行某个请求的时候,若该请求需要一段时间才能返回信息,那么这个进程将会一直等待下去,直到收到返回信息才继续执行下去。
- 异步:指进程不需要一直等下去,而是继续执行下面的操作,不管其他进程的状态。当有消息返回式系统会通知进程进行处理,这样可以提高执行的效率。
1.4 协程
协程是一种用户态的轻量级线程。
子程序,或者称为函数,在所有语言中都是层级调用,比如A调用B,B在执行过程中又调用了C,C执行完毕返回,B执行完毕返回,最后是A执行完毕。所以子程序调用是通过栈实现的,一个线程就是执行一个子程序。
协程看上去也是子程序,但执行过程中,在子程序内部可中断,然后转而执行别的子程序,在适当的时候再返回来接着执行。
例子:
def A():
print('1')
print('2')
print('3')
def B():
print('x')
print('y')
print('z')
假设由协程执行,在执行A的过程中,可以随时中断,去执行B,B也可能在执行过程中中断再去执行A,结果可能是:
1 2 x y 3 z
但是在A中是没有调用B的,看起来A、B的执行有点像多线程,但协程的特点在于是一个线程执行
协程的优势:
- 极高的执行效率:因为子程序切换不是线程切换,而是由程序自身控制,因此,没有线程切换的开销,和多线程比,线程数量越多,协程的性能优势就越明显。
- 不需要多线程的锁机制:因为只有一个线程,也不存在同时写变量冲突,在协程中控制共享资源不加锁,只需要判断状态就好了,所以执行效率比多线程高很多。
1.4 内存分配管理
1.4.1 分段和分页
分段:在段式存储管理中,将程序的地址空间划分为若干段(segment),如代码段,数据段,堆栈段;这样每个进程有一个二维地址空间,相互独立,互不干扰。
分页:在页式存储管理中,将程序的逻辑地址划分为固定大小的页(page),而物理内存划分为同样大小的帧,程序加载时,可以将任意一页放入内存中任意一个帧,这些帧不必连续,从而实现了离散分离。
1.4.2 分段和分页不同点
- 段是信息的逻辑单位,它是根据用户的需要划分的,因此段对用户是可见的 ;页是信息的物理单位,是为了管理主存的方便而划分的,对用户是透明的。
- 段的大小不固定,有它所完成的功能决定;页大大小固定,由系统决定
- 段向用户提供二维地址空间;页向用户提供的是一维地址空间
- 段是信息的逻辑单位,便于存储保护和信息的共享,页的保护和共享受到限制。
- 段式管理的优点是没有内碎片(因为段大小可变,改变段大小来消除内碎片);页式存储管理的优点是没有外碎片(因为页的大小固定),但会产生内碎片(一个页可能填充不满)
1.4.3 堆和栈
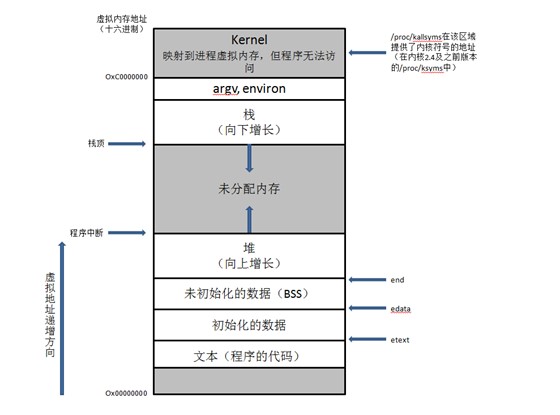
对于一个由C/C++编译的程序,其所占用的内存可以划分为以下几个部分:
-
栈区(stack)—— 由操作系统自动分配和释放,主要用于存放函数参数值,局部变量等。其操作方式类似于数据结构中的栈。
-
堆区(heap)—— 一般由程序员动态分配和释放(malloc,free),若程序员不主动释放,则程序结束后由操作系统回收。注意,它与数据结构中的堆是不同的,分配方式类似于链表。
-
BSS段——主要用于存放未初始化的静态变量和全局变量,可读写,它在程序结束后由操作系统进行释放。
- 数据段(data)——主要用于存放已初始化的静态变量和全局变量,可读写,它在程序结束后由操作系统释放。
- 代码段(text)——主要用于保存程序代码,包括CPU执行的机器指令,同时全局常量也是保存在代码段的,如字符串字面值。
1.4.4 一个进程的内存结构
/main.cpp
int a = 0; // 全局初始化区域
char *p1; // 全局未初始化区域
int main(){
int b; // 栈
char s[] = "adoryn"; // 栈
char *p2; // 栈
char *p3 = "zhaobryant"; // 字符串字面量存放在常量区,p3存放在栈上
static int c = 0; // 全局(静态)初始化区域
p1 = (char *)malloc(10);
p2 = (char *)malloc(20); // 分配获得的10和20字节的内存区放在堆区
strcpy(p1, "zhaobryant"); // 字符串字面量存放在常量区,编译器可能会将它与p3所指向的"zhaobryant"优化为同一个地址
return 0;
}
二. linux相关
2.1 查看CPU和内存占用情况
-
查看物理内存使用情况:
free
-
查看目前正在运行的进程所占的内存百分比和CPU百分比:
top。假如某个进程显示400%,说明该程序利用了4核CPU。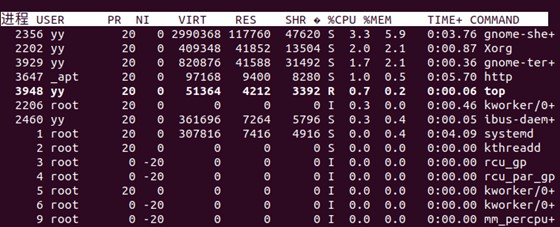
-
查看磁盘使用情况:
df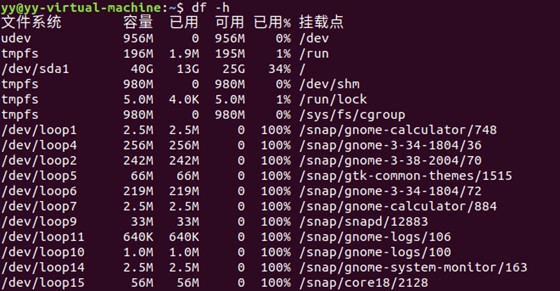
-
查看当前进程:
ps,ps -aux则是当前所有的正在内存当中的程序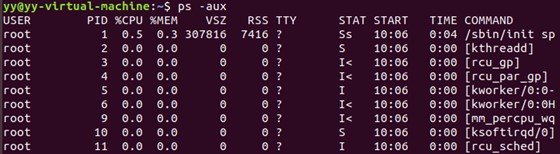
2.2 查找匹配
-
在某个路径下查找是否有某个文件:
find 路径 -name 文件名
-
根据字符串查找相应匹配的文件:
grep。它是一种强大的文本搜索工具,它能使用正则表达式搜索文本,并把匹配的行打印出来。-
查找后缀有 py 字样的文件中包含 print 字符串的文件(当前路径下):
grep print *.py
-
递归查找符合条件的文件,这里是查找指定目录(git_repo)下及其子目录所有文件中包含helloworld字符串的文件

-
联合
ps检查当前进程中python3进程是否运行:ps -aux | grep python3。其中|是管道命令 是指ps命令与grep同时执行。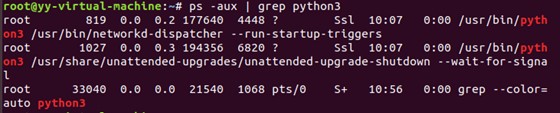
-
2.3 网络相关
-
显示各种网络相关信息:
netstat- 列出所有处于监听状态的Sockets
netstat -l # 只显示监听端口 netstat -lt #只列出所有监听 tcp 端口 netstat -lu #只列出所有监听 udp 端口 netstat -lx #只列出所有监听 UNIX 端口- 配合
grep查找tcp下的指定端口号信息
netstat -plnt | grep :53 # -p 输出中显示 PID 和进程名称 # -l 仅列出有在 Listen (监听) 的服务状态 # -n 不想让主机,端口和用户名显示,而是用ip显示 # -t 只列出所有监听 tcp 端口
2.4 select、poll和epoll
用户空间和内核空间
操作系统的核心是内核,独立于普通的应用程序,可以访问受保护的内存空间,也有访问底层硬件设备的所有权限。
为了保证用户进程不能直接操作内核(kernel),保证内核的安全,操心系统将虚拟空间划分为两部分,一部分为内核空间(供内核使用),一部分为用户空间(供进程使用)。
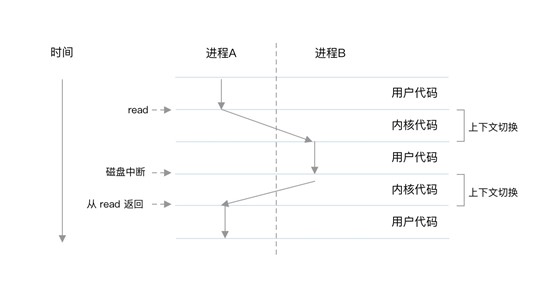
进程切换
为了控制进程的执行,内核必须有能力挂起正在CPU上运行的进程,并恢复以前挂起的某个进程的执行。这种行为被称为进程切换。
进程的切换需要经过以下变换:
- 保存处理机上下文,包括程序计数器和其他寄存器。
- 更新PCB信息。
- 把进程的PCB移入相应的队列,如就绪、在某事件阻塞等队列。
- 选择另一个进程执行,并更新其PCB。
- 更新内存管理的数据结构。
- 恢复处理机上下文。
进程阻塞
正在执行的进程,由于期待的某些事件未发生,如请求系统资源失败、等待某种操作的完成、新数据尚未到达或无新工作做等,则由系统自动执行阻塞原语(Block),使自己由运行状态变为阻塞状态。
进程的阻塞是进程自身的一种主动行为,也因此只有处于运行态的进程(获得CPU),才可能将其转为阻塞状态。当进程进入阻塞状态,是不占用CPU资源的。
文件描述符fd
文件描述符在形式上是一个非负整数。实际上,它是一个索引值,指向内核为每一个进程所维护的该进程打开文件的记录表。
当程序打开一个现有文件或者创建一个新文件时,内核向进程返回一个文件描述符。
缓存IO
在 Linux 的缓存 I/O 机制中,操作系统会将 I/O 的数据缓存在文件系统的页缓存( page cache )中,也就是说,数据会先被拷贝到操作系统内核的缓冲区中,然后才会从操作系统内核的缓冲区拷贝到应用程序的地址空间。
缓存 I/O 的缺点:数据在传输过程中需要在应用程序地址空间和内核进行多次数据拷贝操作,这些数据拷贝操作所带来的 CPU 以及内存开销是非常大的。
Socket
socket是一种”打开—读/写—关闭”模式的实现,服务器和客户端各自维护一个”文件”,在建立连接打开后,可以向自己文件写入内容供对方读取或者读取对方内容,通讯结束时关闭文件。
IO多路复用
IO multiplexing就是我们说的select,poll,epoll。
select/epoll的好处就在于单个process就可以同时处理多个网络连接的IO。它的基本原理就是select,poll,epoll这个function会不断的轮询所负责的所有socket,当某个socket有数据到达了,就通知用户进程。
select
调用后select函数会阻塞,直到有描述副就绪(有数据 可读、可写、或者有except),或者超时(timeout指定等待时间,如果立即返回设为null即可),函数返回。当select函数返回后,可以 通过遍历fdset,来找到就绪的描述符。
select的一 个缺点在于单个进程能够监视的文件描述符的数量存在最大限制,在Linux上一般为1024
poll
不同与select使用三个位图来表示三个fdset的方式,poll使用一个 pollfd的指针实现。
pollfd结构包含了要监视的event和发生的event,不再使用select“参数-值”传递的方式。同时,pollfd并没有最大数量限制(但是数量过大后性能也是会下降)。 和select函数一样,poll返回后,需要轮询pollfd来获取就绪的描述符。
从上面看,select和poll都需要在返回后,通过遍历文件描述符来获取已经就绪的socket。事实上,同时连接的大量客户端在一时刻可能只有很少的处于就绪状态,因此随着监视的描述符数量的增长,其效率也会线性下降。
epoll
相对于select和poll来说,epoll更加灵活,没有描述符限制。epoll使用一个文件描述符管理多个描述符,将用户关系的文件描述符的事件存放到内核的一个事件表中,这样在用户空间和内核空间的copy只需一次。
epoll对文件描述符的操作有两种模式,LT(level trigger)和ET(edge trigger)。LT模式是默认模式,LT模式与ET模式的区别如下:
- LT模式:当epoll_wait检测到描述符事件发生并将此事件通知应用程序,应用程序可以不立即处理该事件。下次调用epoll_wait时,会再次响应应用程序并通知此事件。
- ET模式:当epoll_wait检测到描述符事件发生并将此事件通知应用程序,应用程序必须立即处理该事件。如果不处理,下次调用epoll_wait时,不会再次响应应用程序并通知此事件。
在 select/poll中,进程只有在调用一定的方法后,内核才对所有监视的文件描述符进行扫描,而epoll事先通过epoll_ctl()来注册一 个文件描述符,一旦基于某个文件描述符就绪时,内核会采用类似callback的回调机制,迅速激活这个文件描述符,当进程调用epoll_wait() 时便得到通知。
epoll的优点主要是以下个方面:
- 监视的描述符数量不受限制
- IO的效率不会随着监视fd的数量的增长而下降
2.5 TCP三握四挥
三次握手
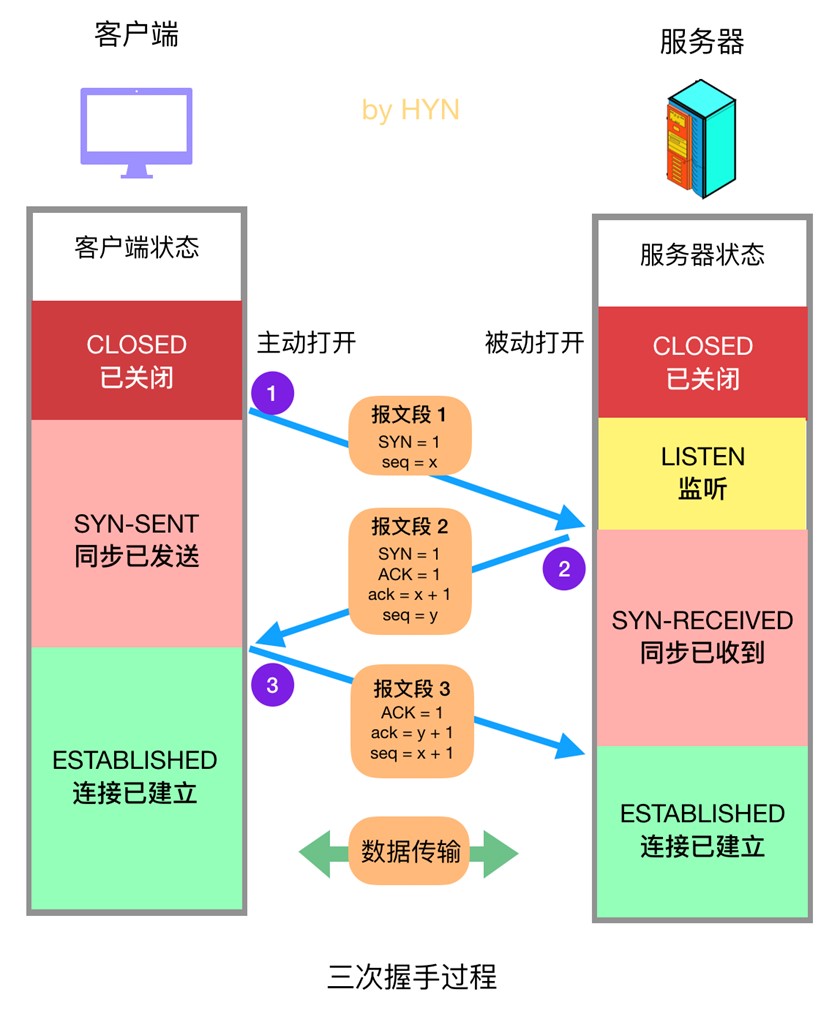
如图所示,双方之间的三个蓝色箭头就表示了三次握手过程中所发生的数据交换:
- 第一次握手:客户端向服务器发送报文段1,其中的 SYN 标志位 (前文已经介绍过各种标志位的作用)的值为 1,表示这是一个用于请求发起连接的报文段,其中的序号字段 (Sequence Number,图中简写为seq)被设置为初始序号x (Initial Sequence Number,ISN),TCP 连接双方均可随机选择初始序号。发送完报文段1之后,客户端进入 SYN-SENT 状态,等待服务器的确认。
- 第二次握手:服务器在收到客户端的连接请求后,向客户端发送报文段2作为应答,其中 ACK 标志位设置为 1,表示对客户端做出应答,其确认序号字段 (Acknowledgment Number,图中简写为小写 ack) 生效,该字段值为 x + 1,也就是从客户端收到的报文段的序号加一,代表服务器期望下次收到客户端的数据的序号。此外,报文段2的 SYN 标志位也设置为1,代表这同时也是一个用于发起连接的报文段,序号 seq 设置为服务器初始序号y。发送完报文段2后,服务器进入 SYN-RECEIVED 状态。
- 第三次握手:客户端在收到报文段2后,向服务器发送报文段3,其 ACK 标志位为1,代表对服务器做出应答,确认序号字段 ack 为 y + 1,序号字段 seq 为 x + 1。此报文段发送完毕后,双方都进入 ESTABLISHED 状态,表示连接已建立。
常见面试题 1: TCP 建立连接为什么要三次握手而不是两次?
- 防止已过期的连接请求报文突然又传送到服务器,因而产生错误
- 三次握手才能让双方均确认自己和对方的发送和接收能力都正常
- 告知对方自己的初始序号值,并确认收到对方的初始序号值
常见面试题2: TCP 建立连接为什么要三次握手而不是四次?
- 相比上个问题而言,这个问题就简单多了。因为三次握手已经可以确认双方的发送接收能力正常,双方都知道彼此已经准备好,而且也可以完成对双方初始序号值得确认,也就无需再第四次握手了。
四次挥手
建立一个连接需要三次握手,而终止一个连接要经过 4次握手。这由 TCP 的半关闭( half-close) 造成的。既然一个 TCP 连接是全双工 (即数据在两个方向上能同时传递), 因此每个方向必须单独地进行关闭。
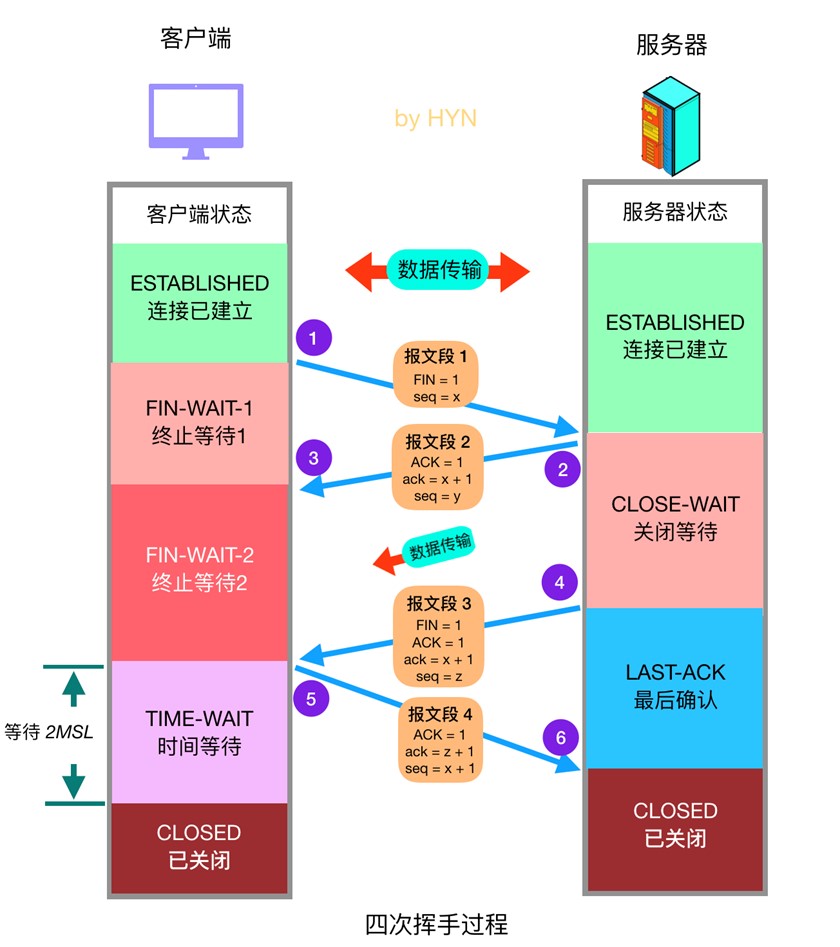
四次挥手详细过程如下:
- 客户端发送关闭连接的报文段,FIN 标志位1,请求关闭连接,并停止发送数据。序号字段 seq = x (等于之前发送的所有数据的最后一个字节的序号加一),然后客户端会进入 FIN-WAIT-1 状态,等待来自服务器的确认报文。
- 服务器收到 FIN 报文后,发回确认报文,ACK = 1, ack = x + 1,并带上自己的序号 seq = y,然后服务器就进入 CLOSE-WAIT 状态。服务器还会通知上层的应用程序对方已经释放连接,此时 TCP 处于半关闭状态,也就是说客户端已经没有数据要发送了,但是服务器还可以发送数据,客户端也还能够接收。
- 客户端收到服务器的 ACK 报文段后随即进入 FIN-WAIT-2 状态,此时还能收到来自服务器的数据,直到收到 FIN 报文段。
- 服务器发送完所有数据后,会向客户端发送 FIN 报文段,各字段值如图所示,随后服务器进入 LAST-ACK 状态,等待来自客户端的确认报文段。
- 客户端收到来自服务器的 FIN 报文段后,向服务器发送 ACK 报文,随后进入 TIME-WAIT 状态,等待 2MSL(2 * Maximum Segment Lifetime,两倍的报文段最大存活时间) ,这是任何报文段在被丢弃前能在网络中存在的最长时间,常用值有30秒、1分钟和2分钟。如无特殊情况,客户端会进入 CLOSED 状态。
- 服务器在接收到客户端的 ACK 报文后会随即进入 CLOSED 状态,由于没有等待时间,一般而言,服务器比客户端更早进入 CLOSED 状态。
三. C++
3.1 STL中list,vector,map,set区别
vector
- vector封装了数组,拥有一段连续的内存空间,并且起始地址不变。
- 存取复杂度:能实现高效的随机存取,其时间复杂度为O(1)。
- 增删复杂度:由于内存空间是连续的,因此插入和删除时,会造成内存块的拷贝,时间复杂度为O(n)。
- 特别是当数组空间不足时,会重新申请一块内存空间(2倍)并进行拷贝。
- vector支持根据下标随机存取元素。其原因是“循秩访问”这种向量特有的元素访问方式。
list
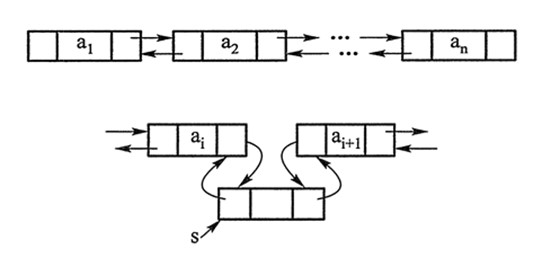
- list 封装了链表,且是双向链表。因此内存空间是不连续的。
- 每一个结点都维护一个信息块、一个前向指针和一个后向指针,因此支持前向/后向遍历。
- 存取复杂度:只能通过指针访问数据,所以list的随机存取非常没有效率,时间复杂度为o(n)。原因是存储的对象是离散的,随机访问需要遍历整个链表
- 增删复杂度:在已经定位到要增删元素的位置的情况下,增删元素能在常数时间内完成,即O(1) 。可以不分配必须的内存大小方便的进行添加和删除操作。
- 当要存储的是大型负责类对象时,list要优于vector。
-
list 容器不支持根据下标随机存取元素。不支持[ ]操作符和vector.at()。
map
- map的本质其实就是映射,键值(key-value)一一对应。
- map的实现是一颗红黑树,因此,map的内部键的数据都是排好序的,查找和删除、插入的效率都是n(logn)。
- multimap 允许一个键对应多个值;而map则是一个键对应一个值。
set
- 所得元素的只有key没有value,value就是key。不允许键值的重复,即在set中每个元素的值都唯一。
- set的实现是一颗红黑树,因此,set的内部键的数据都是排好序的,查找和删除、插入的效率都是n(logn)。
- set不能通过迭代器修改set元素值,其原因是set的值就是键。
3.2 虚函数
虚函数使用条件
当基类指针指向一个子类对象,通过这个指针调用子类和基类同名成员函数的时候,基类声明为虚函数「子类不写也可以」就会调子类的这个函数,不声明就会调用基类的。关键字:virtual

构造和析构可以是虚函数么
构造不能为虚函数:如果构造函数是虚函数,那么就需要通过vtable(虚函数指针表) 来调用,但此时面对一块 raw memeory,到哪里去找 vtable 呢?毕竟,vtable 是在构造函数中才初始化的啊,而不是在其之前。因此构造函数不能为虚函数。
析构为虚函数:此时 vtable 已经初始化了;况且我们通常通过基类的指针来销毁对象,如果析构函数不为虚的话,就不能正确识别对象类型,从而不能正确销毁对象。
虚函数可以是内联函数(inline)么
-
内联函数:由于函数调用耗时长,因此在编译时将所调用的函数的代码直接嵌入到主调函数中,可以理解为内联函数体代码直接替换了调用函数这行代码。
- 虚函数可以是内联函数,内联是可以修饰虚函数的,但是当虚函数表现多态性的时候不能内联。
- 内联是在编译器建议编译器内联,而虚函数的多态性在运行期,编译器无法知道运行期调用哪个代码,因此虚函数表现为多态性时(运行期)不可以内联。
3.3 继承和多态
C++有其三大特性:封装、继承和多态。
继承
以让某个类型的对象,获得另一种类型对象属性的方法。实际上就是类与类之间可以共用代码,实现代码重用。可以理解为子类继承父类的方法。
例子:父类为Animal,其仅有2个成员函数,分别为bark()和eat()。子类为Dog,继承了父类的bark()和eat(),同时它还有自己的另一个方法run()。
多态
多种形态,指一个类实例的相同方法在不同情况下有不同表现形式。
即子类可以重写父类的某个函数,从而为这个函数提供不同于父类的行为。一个父类的多个子类可以为同一个函数提供不同的实现,从而在父类这个公共的接口下,表现出多种行为。
例子:父类为Animal,其仅有2个成员函数,分别为bark()和eat()。子类为Dog,Cat,Snake,对于同一个方法bark()而言,不同的子类存在不同的喊叫方式,即为多态。
区别
- 多态的实现要求必须是共有继承。
- 继承关系中,并不要求基类方法一定是虚函数。而多态时,要求基类方法必须是虚函数。
- 多态:子类重写父类的方法,使得子类具有不同的实现。且运行时,根据实际创建的对象动态决定使用哪个方法。
四. 数据结构和算法
4.1 排序算法
排序算法可以分为两大类:
- 比较类排序:通过比较来决定元素间的相对次序,由于其时间复杂度不能突破O(nlogn),因此也称为非线性时间比较类排序。这里比如冒泡、插入、快排、归并、堆排序等。
- 非比较类排序:不通过比较来决定元素间的相对次序,它可以突破基于比较排序的时间下界,以线性时间运行,因此也称为线性时间非比较类排序。 这里比如计数排序和位图排序。
算法复杂度
| 排序方法 | 时间复杂度(平均) | 时间复杂度(最坏) | 时间复杂度(最好) | 空间复杂度 | 稳定性 |
|---|---|---|---|---|---|
| 冒泡排序 | 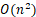 |
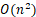 |
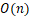 |
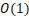 |
稳定 |
| 插入排序 | 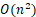 |
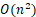 |
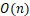 |
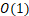 |
稳定 |
| 快速排序 | 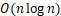 |
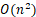 |
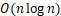 |
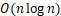 |
不稳定 |
| 归并排序 | 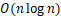 |
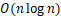 |
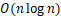 |
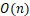 |
稳定 |
| 堆排序 | 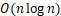 |
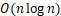 |
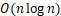 |
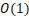 |
不稳定 |
| 计数排序 | 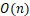 |
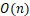 |
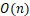 |
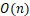 |
稳定 |
| 位图排序 | 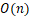 |
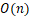 |
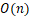 |
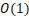 |
稳定 |
冒泡排序 Bubble sort
它重复地走访过要排序的数列,一次比较两个元素,如果它们的顺序错误就把它们交换过来。走访数列的工作是重复地进行直到没有再需要交换,也就是说该数列已经排序完成。
算法步骤:
- 比较相邻的元素。如果第一个比第二个大,就交换它们两个;
- 对每一对相邻元素作同样的工作,从开始第一对到结尾的最后一对,这样在最后的元素应该会是最大的数;
- 针对所有的元素重复以上的步骤,除了最后一个;
- 重复步骤1~3,直到排序完成。
插入排序 Insertion Sort
它的工作原理是通过构建有序序列,对于未排序数据,在已排序序列中从后向前扫描,找到相应位置并插入。
算法步骤:
- 从第一个元素开始,该元素可以认为已经被排序;
- 取出下一个元素,在已经排序的元素序列中从后向前扫描;
- 如果该元素(已排序)大于新元素,将该元素移到下一位置;
- 重复步骤3,直到找到已排序的元素小于或者等于新元素的位置;
- 将新元素插入到该位置后;
- 重复步骤2~5。
快速排序 Quick Sort
通过一趟排序将待排记录分隔成独立的两部分,其中一部分记录的关键字均比另一部分的关键字小,则可分别对这两部分记录继续进行排序,以达到整个序列有序。快速排序使用分治法来把一个串(list)分为两个子串(sub-lists)。
算法步骤:
- 从数列中挑出一个元素,称为 “基准”(pivot);
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作;
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序。
归并排序 Merge Sort
该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为2-路归并。
算法步骤:
- 把长度为n的输入序列分成两个长度为n/2的子序列;
- 对这两个子序列分别采用归并排序;
- 将两个排序好的子序列合并成一个最终的排序序列。
堆排序 Heap Sort
利用堆这种数据结构所设计的一种排序算法。堆积是一个近似完全二叉树的结构,并同时满足堆积的性质:即子结点的键值或索引总是小于(或者大于)它的父节点,大顶堆和小顶堆。
算法步骤:
- 将初始待排序关键字序列(R1,R2….Rn)构建成大顶堆,此堆为初始的无序区;
- 将堆顶元素R[1]与最后一个元素R[n]交换,此时得到新的无序区(R1,R2,……Rn-1)和新的有序区(Rn),且满足R[1,2…n-1]<=R[n];
- 由于交换后新的堆顶R[1]可能违反堆的性质,因此需要对当前无序区(R1,R2,……Rn-1)调整为新堆,然后再次将R[1]与无序区最后一个元素交换,得到新的无序区(R1,R2….Rn-2)和新的有序区(Rn-1,Rn)。不断重复此过程直到有序区的元素个数为n-1,则整个排序过程完成。
计数排序 Counting Sort
计数排序不是基于比较的排序算法,其核心在于将输入的数据值转化为键存储在额外开辟的数组空间中。 作为一种线性时间复杂度的排序,计数排序要求输入的数据必须是有确定范围的整数。
算法步骤:
- 找出待排序的数组中最大和最小的元素;
- 统计数组中每个值为i的元素出现的次数,存入数组C的第i项;
- 对所有的计数累加(从C中的第一个元素开始,每一项和前一项相加);
- 反向填充目标数组:将每个元素i放在新数组的第C(i)项,每放一个元素就将C(i)减去1。
位图排序 Bitmap Sort
位图排序是一种效率极高(复杂度可达O(n))并且很节省空间的一种排序方法,但是这种排序方法对输入的数据是有比较严格的要求(数据不能重复,大致知道数据的范围)。 位图排序即利用位图或者位向量来表示集合。
参考的面试题:40亿个QQ号码,如果使用O(1)的时间复杂度去查找一个QQ号是否存在。
算法步骤:
- 根据待排序集合中最大的数,开辟一个位数组,用来表示待排序集合中的整数。
- 待排序集合中的数字在位数组中的对应位置置1,其他的置0。
- 将对应序号的整数放置到位对应的index上,并在每个对应的位上置位1.
- 检验每一位,如果该位位1,输出对应的整数。
4.2 红黑树
二叉查找树(BST)
特性:
-
左子树上所有结点的值均小于或等于它的根结点的值。
-
右子树上所有结点的值均大于或等于它的根结点的值。
-
左、右子树也分别为二叉排序树。
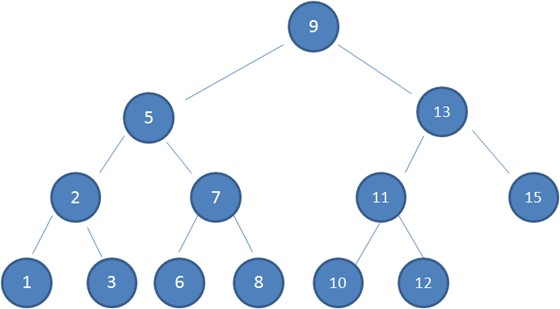
根据二分查找的思想,查找的最大次数等同于树的高度。但是二叉查找树有其自身的缺陷:在多次出入新的节点后可能会出现不平衡现象,如下图。
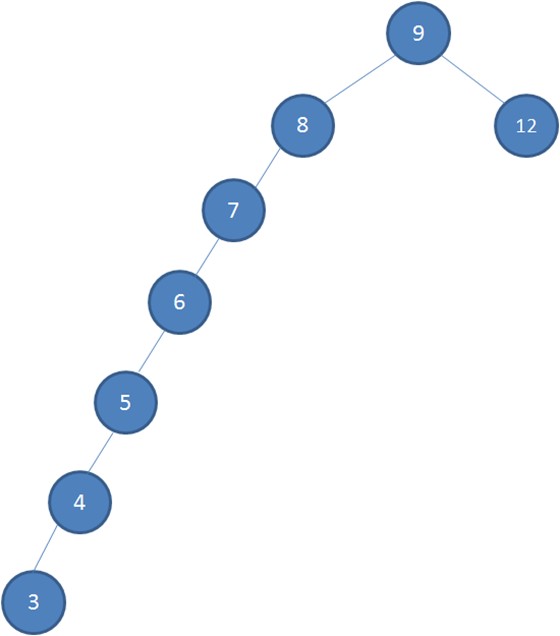
红黑树(RBT)
红黑树是一种自平衡的二叉查找树。其除了具有二查找树的特性外,还具有以下特性:
- 节点是红色或黑色。
- 根节点是黑色。
- 每个叶子节点都是黑色的空节点(NIL节点)。
- 每个红色节点的两个子节点都是黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
- 从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点。
如下图插入一个14的新节点。
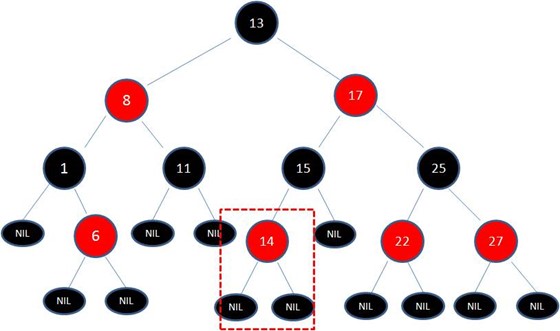
红黑树实现自平衡的三种操作:
-
左旋:逆时针旋转红黑树的两个节点,使得父节点被自己的右孩子取代,而自己成为自己的左孩子。
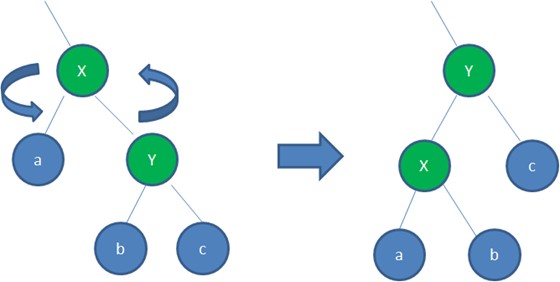
-
右旋:顺时针旋转红黑树的两个节点,使得父节点被自己的左孩子取代,而自己成为自己的右孩子。
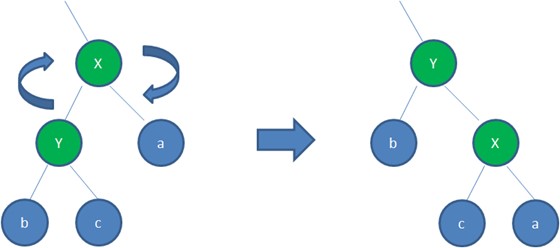
-
变色
4.3 回溯算法
递归实现-伪代码
算法 ReBack(k)
if k>n:
then <x1,x2...xn>是解
else:
while S_k != 空集 do
找到S_k中的最小值x_k
S_k = S_k - {x_k}
计算S_k+1
ReBack(k+1)
迭代实现-伪代码
迭代算法 Backtrack
输入:n
输出:所有的解
1. 对于i=1,2,...n 确定x_i # 确定初始值
2. k = 1
3. 计算S_k
4. while S_k != 空集 do # 满足约束分支搜索
找到S_k中的最小值x_k
S_k = S_k - {x_k}
if k < n then
k = k+1
计算S_k
else
<x1,x2...xn>是解
5. if k>1 then k = k-1 ; goto4 # 回溯
四后问题
问题描述:在4 * 4 的方格棋盘中放置4个皇后,使得没有2个皇后在同一行、同一列、也不在45°的斜线上。问有多少种可能的布局?

解是4维向量<x_1,x_2,x_3,x_4>,解为:<2,4,1,3>,<3,1,4,2>
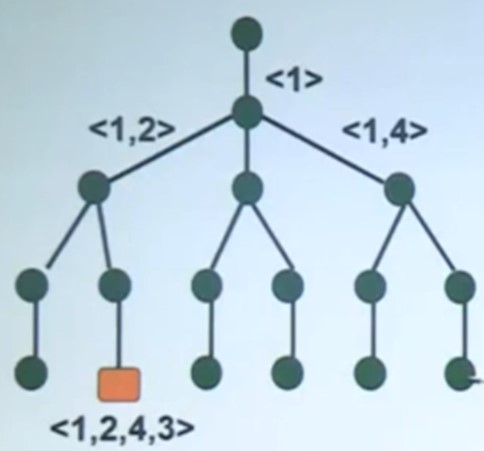
其搜索空间是一个4叉树,如下图。
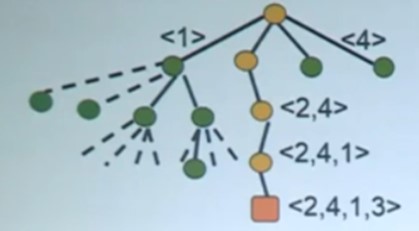
- 每个结点有4个儿子,分别代表1,2,3,4列位置。
- 第 i 层选择解向量中第 i 个分量的值
- 最深层的树叶是解。
- 按深度优先次序便利树,找到所有的解。
0-1背包问题
问题描述:有n种物品,每种物品只有1个。第 i 种物品价值为v_i,重量位w_i,i = 1,2,…,n。问如何选择放入背包的物品,使得总重量不超过B,而价值达到最大?
解:n维 0-1 向量<x_1,x_2,…x_n>
节点:<x_1,x_2,…x_k>
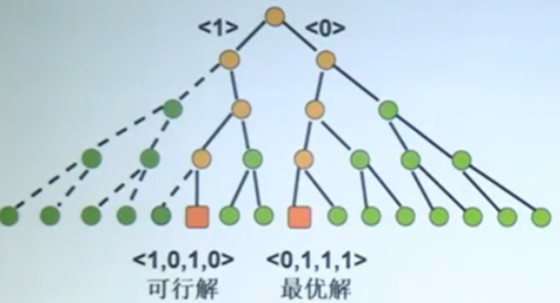
搜索空间: 0-1 取值的二叉树,称为子集树,有2^n 片树叶。
可行解:满足约束条件 \(\sum_{i=1}^{n} w_{i} x_{i} \leq B\) 最优解:可行解中价值达到最大的解
实例:V = {12,11,9,8},W = {8,6,4,3},B = 13
货郎问题
问题描述:有n个城市,已知任两个城市之间的距离,求一条每个城市恰好经过一次的回路,使得总长度最小。
实例:City = {1,2,3,4},d(1,2) = 5,d(1,3) = 9,d(1,4) = 4,d(2,3) = 13,d(2,4) = 2,d(3,4) = 7。
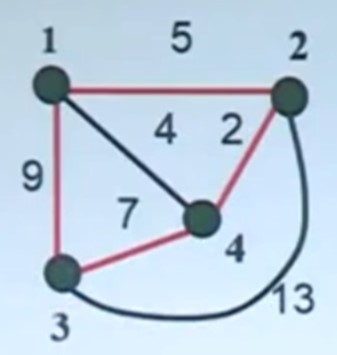
解:<1,2,4,3> 长度 = 5 + 2 + 7 + 9 = 23
搜索空间:排列树,每层有 (n-1)! 片树叶