贝叶斯公式及模型的理解
一. 贝叶斯公式
1.1 实际的例子推导公式
这里我们用比较实际的例子来理解贝叶斯公式。
现在我们有2个骰子,每个骰子有6个面。
- 样本空间:$6\times6 = 36$
- 事件A:其中一个骰子展示的是2
- 事件B:两个骰子的总和是7
如下图所示,将所有的样本空间展示出来,并圈出事件A、B两种情况的所有可能性。

那么,针对每个不同的事件所发生的概率如下:
-
事件A发生的概率:

-
事件B发生的概率:

-
事件A、B同时发生的概率:

-
在A发生的条件下,B发生的概率:

-
在B发生的条件下,A发生的概率:

因此我们可以发现:
-
$A和B同时发生的概率 = 在B发生条件下A发生的概率 \times B发生的概率$,如下

-
$A和B同时发生的概率 = 在A发生条件下B发生的概率 \times A发生的概率$,如下

-
由上面2个式子,可得$在B发生条件下A发生的概率 \times B发生的概率 = 在A发生条件下B发生的概率 \times A发生的概率$,即得到了贝叶斯公式,如下。
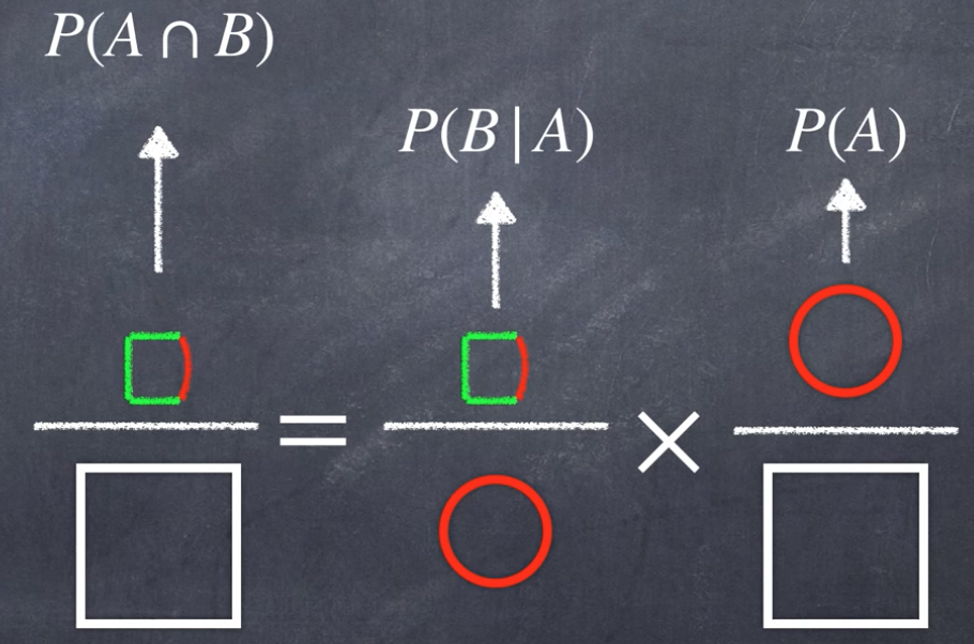
1.2 用图来理解贝叶斯公式
接下来我们利用图的更好的理解贝叶斯公式。
- 白色的矩形:表示整个样本空间
- 红色的圆:表示A事件
- 绿色的长方形:表示B事件
- 圆和长方形交集:表示A事件和B事件同时发生时的事件。

那么交集事件的概率就如下所示:
-
$A和B同时发生的概率 = 在B发生条件下A发生的概率 \times B发生的概率$

-
$A和B同时发生的概率 = 在A发生条件下B发生的概率 \times A发生的概率$
二. 朴素贝叶斯模型
2.1 真实案例——泰坦尼克生存者预测
我们这里选择kaggle竞赛的一个Titanic生存率预测来说明下朴素贝叶斯是如何构建概率模型的。
这里简单的构建了一个小型的数据集如下:
| survival($Y$) | age > 18($x_1$) | pclass = 1($x_2$) | sex = male($x_3$) |
|---|---|---|---|
| 1 | 1 | 1 | 1 |
| 0 | 0 | 0 | 1 |
| 1 | 1 | 1 | 0 |
| 0 | 0 | 1 | 0 |
| 1 | 1 | 0 | 1 |
| 0 | 0 | 1 | 1 |
| 1 | 1 | 0 | 0 |
| 0 | 0 | 0 | 0 |
那么对于一条新的样本:age = 20 , pclass = 2 , sex = female的乘客而言,她能生存下来么?
2.2 朴素贝叶斯模型推导
对于上述的新样本的预测问题,我们转化成概率问题,即 \(P(Y|x_1,x_2,x_3) = ?\)
- 这里利用贝叶斯公式转化,即:
-
由于$x_1,x_2,x_3$出现的概率为1,因此,上式简化为: \(P(Y|x_1,x_2,x_3) = P(x_1,x_2,x_3|Y) \times P(Y)\)
-
这里引入朴素的思想:假定每个特征条件($x_1,x_2,x_3$)之间相互独立。那么:
- 通过计算得到:
-
$P(x_1 = 1 Y = 1) = \frac{4}{4} = 1$ -
$P(x_2 = 0 Y = 1) = \frac{2}{4} = 0.5$ -
$P(x_3 = 0 Y = 1) = \frac{2}{4} = 0.5$ - $P(Y = 1) = \frac{4}{8} = 0.5$
-
- 因此,对于age = 20 , pclass = 2 , sex = female的乘客而言,她能生存的概率为: \(P(Y = 1|x_1 = 1,x_2 = 0,x_3 = 0) = 1 \times 0.5 \times 0.5\times 0.5 = 0.125\)
