无监督异常检测模型
异常检测模型一般分为五大类:统计和概率模型、线性模型、非线性模型、基于相似度衡量的模型、基于聚类的异常检测模型。
一. 统计和概率模型
主要是假设和检验。假设数据的分布,检验异常。比如对一维的数据假设高斯分布,然后将3sigma以外的数据划分为异常,上升到高维,假设特征之间是独立的,可以计算每个特征维度的异常值并相加,如果特征之间是相关的,也就变成了多元高斯分布,可以用马氏距离衡量数据的异常度。这 类方法要求对问题和数据分布有较强的先验知识。
1.1 3σ原则
如果特征服从正态分布,那么,在\(\pm 3 \sigma\)的范围内包含了99.73%的“几乎所有”的内容(所有正常的值都在平均值正负三个标准差的范围内),而可能存在的异常值都在其之外。
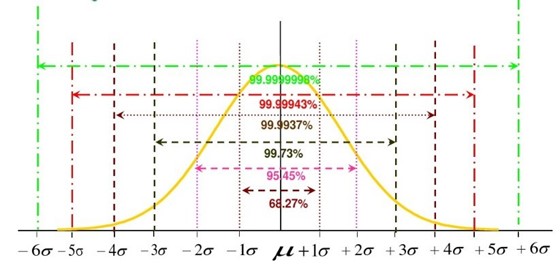
1.2 3σ原则的适用条件
- 数据分布满足正态分布(在业务逻辑上母样本满足)。
- 特征之间相互独立。
二. 线性模型
2.1 PCA
PCA是最常见的线性降维方法,它们按照某种准则为数据集 \(\left\{x_{i}\right\}_{i=1}^{n}\) 找到一个最优投影方向 W 和截距和截距 b ,然后做变换 \(z_{i}=W x_{i}+b\) 得到降维后的数据集 \(\left\{z_{i}\right\}_{i=1}^{n}\) 。因为 \(z_{i}=W x_{i}+b\) 是一个线性变换(严格来说叫仿射变换,因为有截距项),因此PCA属于线性模型(处理线性问题)。
假设数据在低维空间上有嵌入,那么无法、或者在低维空间投射后表现不好的数据可以认为是异常点。PCA有两种检测异常的方法,一种是将数据映射到低维空间,然后在特征空间不同维度上查看每个数据点和其他数据点的偏差,另一种是看重构误差,先映射到低维再映射回高维,异常点的重构误差较大。这两种方法的本质一样,都是关注较小特征值对应的特征向量方向上的信息。
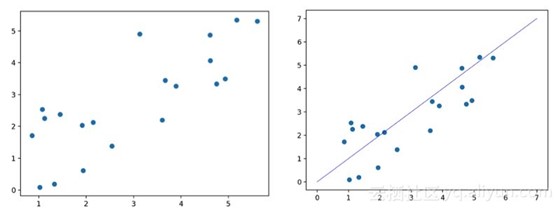
可以利用PCA将二维的特征数据映射到一维上(尽量保持原始信息),然后再映射到二维空间,对比重构的二维数据和初始的二维数据的误差值(MSE),设定阈值,大于阈值的为异常,小于等于阈值的为正常。
- 模型构建过程:
- 原始数据: \(x_{i} \in R^{d}\)
- 编码后的数据: \(z_{i}=W^{T}\left(x_{i}+b\right) \in R^{c}\)
- 解码后的数据: \(\hat{x}_{i}=W z_{i}-b \in R^{d}\)
- 重构的误差: \(\sum_{i=1}^{n}\left\|x_{i}-\hat{x}_{i}\right\|_{p}^{p}\)
2.2 OneClass-SVM
- (1)与传统SVM不同的是,one class SVM是一种非监督的算法。它是指在训练集中只有一类positive(或者negative)的数据,而没有另外的一类。而这时,需要学习(learn)的就是边界(boundary),而不是最大间隔(maximum margin)。
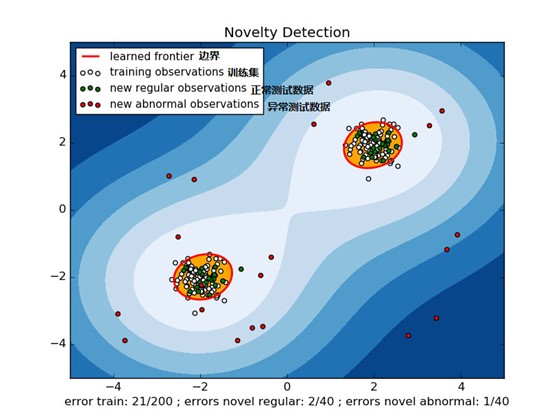
- (2)与传统SVM不同的是,one class SVM是一种非监督的算法。它是指在训练集中只有一类positive(或者negative)的数据,而没有另外的一类。而这时,需要学习(learn)的就是边界(boundary),而不是最大间隔(maximum margin)。与传统SVM不同的是,one class SVM是一种非监督的算法。它是指在训练集中只有一类positive(或者negative)的数据,而没有另外的一类。而这时,需要学习(learn)的就是边界(boundary),而不是最大间隔(maximum margin)。

三. 非线性模型
3.1 AutoEncoder
非线性降维的代表方法是AutoEncoders,AutoEncoders的非线性和神经网络的非线性是一回事,都是利用堆叠非线性激活函数来近似任意函数。事实上,AutoEncoders就是一种神经网络,只不过它的输入和输出相同,真正有意义的地方不在于网络的输出,而是在于网络的权重。
- 模型构建过程:
-
原始数据: \(x_{i} \in R^{d}\)
-
编码后的数据: \(z_{i}=\sigma\left(W^{T} x_{i}+b\right) \in R^{c}\)
-
解码后的数据: \(\hat{x}_{i}=\hat{\sigma}\left(\hat{W} z_{i}+\hat{b}\right) \in R^{d}\)
-
重构的误差: \(\sum_{i=1}^{n}\left\|x_{i}-\hat{x}_{i}\right\|_{p}^{p}\)
-
这里sigma是非线性激活函数。AutoEncoder一般都会堆叠多层(多层神经层同样也能增加模型的非线性),方便起见我们只写了一层。
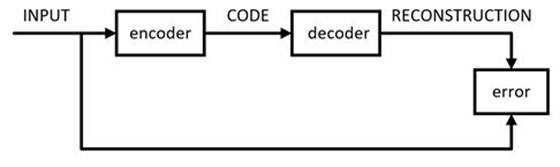
Autoencoder可以参与构建2种不同的异常检测模型。
- (1)非线性降维:利用训练好的模型参数,通过输入到Encoder中,直接输出中间的CODE,而这个CODE就是数据经过非线性降维后的数据,然后利用降维后的数据放入到常用的聚类算法中(比如KMeans),搭建无监督异常检测模型。
- (2)本身作为异常值的判别器:在训练好的模型之后,数据通过Encoder映射到低维空间后,利用Decoder重构回高维空间,而当输入数据是异常数据的时候,重构的高维数据会和原始数据的loss(MSE)很高,在这里设定一个阈值,大于阈值的为异常,小于等于阈值的为正常。
3.2 VAE(Variational AutoEncoder)
Variational AutoEncoder(VAE)是由 Kingma 和 Welling 在“Auto-Encoding Variational Bayes, 2014”中提出的一种生成模型。
VAE其实可以看作AutoEncoder的一个变种,它在AutoEncoder区别在于在Encoder映射到低维空间中映射成了2个Vector,一个属于原始的CODE,而另一个作为噪声增加到新的CODE中。
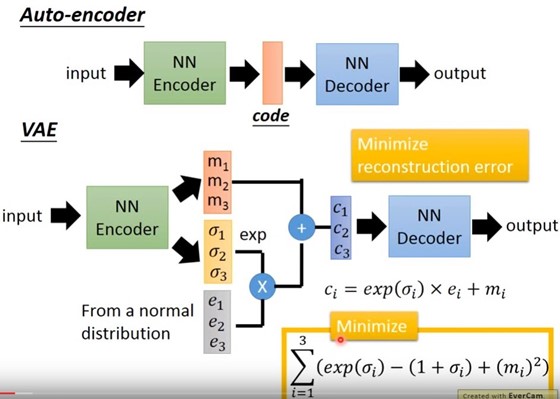
上图中,M_1,M_2,M_3作为Original Code,sigma_1,sigma_2,sigma_3这种变分的噪点则是通过模型自动训练学习得到的,e_1,e_2,e_3定义为服从一个标准的正太分布的向量,那么在AutoEncoder中的低维空间code在VAE中就是上图中的c_i了。
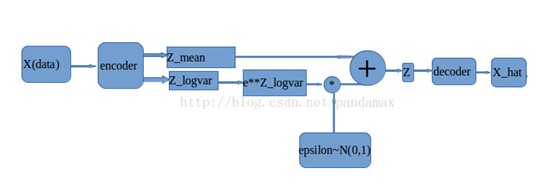
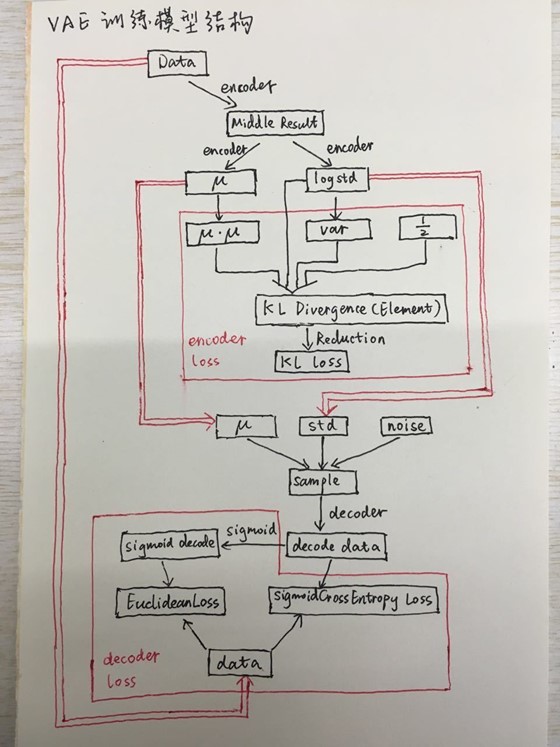
code的定义公式如下: \(c_{i}=\exp \left(\sigma_{i}\right) \times e_{i}+m_{i}\)
当然,对于VAE来说,定义loss的function也和AutoEncoder不一样: \(loss=\sum_{i=1}^{3}\left(\exp \left(\sigma_{i}\right)-\left(1+\sigma_{i}\right)+\left(m_{i}\right)^{2}\right)\)
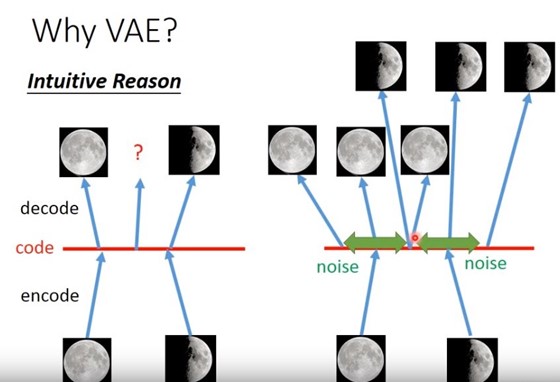
VAE相较于AutoEncoder的优势在于:映射到低维空间的code增加了噪声,导致重构的高维空间中的值可以和原始数据不太一样,比如AutoEncoder模型原始输入是满月和斜月,那么输出一定是满月和斜月,而VAE则是可以生成满月和斜月的结合体。
四. 基于划分超平面的模型——Isolation Forest
4.1 孤立森林的思想是
假设我们用一个随机超平面来切割(split)数据空间(data space), 切一次可以生成两个子空间(想象拿刀切蛋糕一分为二)。之后我们再继续用一个随机超平面来切割每个子空间,循环下去,直到每子空间里面只有一个数据点为止。直观上来讲,我们可以发现那些密度很高的簇是可以被切很多次才会停止切割,但是那些密度很低的点很容易很早的就停到一个子空间了。
4.2 孤立森林的优势
孤立森林算法具有线性时间复杂度。因为是ensemble的方法,所以可以用在含有海量数据的数据集上面。通常树的数量越多,算法越稳定。由于每棵树都是互相独立生成的,因此可以部署在大规模分布式系统上来加速运算。
4.3 孤立森林的劣势
孤立森林不适用于特别高维的数据。由于每次切数据空间都是随机选取一个维度,建完树后仍然有大量的维度信息没有被使用,导致算法可靠性降低。高维空间还可能存在大量噪音维度或无关维度(irrelevant attributes),影响树的构建。
五. 基于聚类的异常检测模型
5.1 常用的聚类算法
- (1)KMeans:利用找到的簇的中心点和每一个样本的距离值,找到最偏离簇中心的点作为异常点。
- (2)DBSCAN–基于密度的聚类:由于需要涉及到算法本身两个参数(min_samples和eps),这里模型会直接输出超过半径eps和确定好最小数的min_samples的样本点作为异常值(label = -1)。
- (3)Birch–基于层次的聚类:BIRCH算法利用了一个树结构来帮助我们快速的聚类,这个数结构类似于平衡B+树,一般将它称之为聚类特征树(Clustering Feature Tree,简称CF Tree)。建立好CF Tree后把那些包含数据点少的MinCluster当作outlier。
5.2 聚类算法的适应性
每一种算法对于不同的数据分布可能存在不同优势。
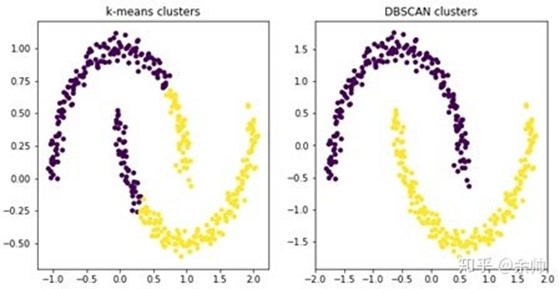
K-Means算法对于凸性数据具有良好的效果,能够根据距离来讲数据分为球状类的簇,但对于非凸形状的数据点,就无能为力了,比如环形数据等等,此时基于密度的算法DBSCAN就更令人满意了。

5.2 评价聚类效果指标
聚类算法的目标是:簇内相似度高,簇间相似度低。
因此通过轮廓系数(Silhouette Coefficient)来评价聚类效果的好坏,适用于上述三种算法。 1、将样本x与簇内的其他点之间的平均距离作为簇内的内聚度a 2、将样本x与最近簇中所有点之间的平均距离看作是与最近簇的分离度b 3、将簇的分离度与簇内聚度之差除以二者中比较大的数得到轮廓系数,计算公式如下 \(s^{(i)}=\frac{b^{(i)}-a^{(i)}}{\max \left\{b^{(i)}, a^{(i)}\right\}}\) 轮廓系数的取值在-1到1之间。当簇内聚度与分度离相等时,轮廓系数为0。当b»a时,轮廓系数近似取到1,此时模型的性能最佳。
